
Функционально-градиентная термопара
Одним из направлений повышения эффективности термопар является использование в ветвях материалов, у которых свойства являются функциями координат. Такие материалы принято называть функционально-градиентными материалами. На перспективу использования неоднородных ветвей указывал еще академик Иоффе в своей книге "Полупроводниковые термоэлементы" [26].
Проектирование термоэлементов из функциональноградиентных материалов изложено в работах [11, 72, 73, 111].
Целью проектирования является нахождение распределения концентрации примеси вдоль ветви, при которой при заданных Th и Тс достигается максимальный коэффициент полезного действия или максимальная мощность.
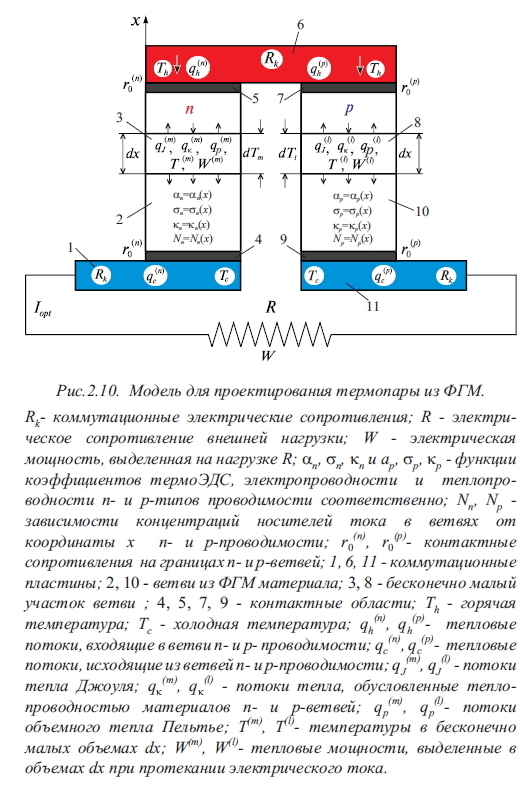
Физическая модель для компьютерного проектирования термопары из ФГМ материала приведена нарис.2.10. В модели использованы неоднородные ветви n- и p-типа проводимости, включенные в электрическую и тепловую цепь, внешняя оптимальная электрическая нагрузка Ropt, на которой выделяется электрическая мощность W. При расчетах учитывается выделение тепла Джоуля в объеме ветви, перенос тепла теплопроводностью в ветвях, выделение объемного тепла Пельтье и выделение электрической мощности за счет внутренних термоэлектродвижущих сил, вызванных изменением коэффициента Зеебека вдоль ветви. В модели учитываются контактные сопротивления r0(np), а также электрические потери в коммутационных пластинах с электрическим сопротивлением Rk. Исходная система уравнений, описывающая тепловые и электрические процессы в бесконечно малой части ветви dx, дается выражениями

Уравнения написаны на основе закона сохранения энергии и дифференциального закона Ома для цепи с термоэлектрическими источниками.
Из решения системы уравнений (2.51), (2.52) могут быть найдены распределения температуры в ветвях

Решение такой задачи проводится численно путем использования комбинации метода Ейлера и метода стрельбы для системы дифференциальных уравнений (2.51).
Наибольшее значение КПД достигается при использовании оптимальных функций неоднородности материала. Такие функции определяются расчетным путем. Для этого созданы специальные компьютерные программы. Они основаны на применении метода оптимального управления Понтрягина [50]. Суть метода сводится к тому, что вначале используется нулевое приближение искомой функции в виде независящих от координаты параметров материала Nn и Np. Метод Понтрягина сводится к поиску оптимальных функций путем расчета КПД для различных функций, отличных от заданных нулевых. Метод Понтрягина позволяет вести целенаправленный поиск таких функции. Оптимальные функции Nnp(x) определяются из условия


При расчетах вместо связей (2.55) - (2.60) часто используют экспериментальные зависимости параметров материала от концентрации примесей и температуры.


Конкретные виды функций ФГМ материалов, определенные по изложенной выше методике, приведены в работах [11, 72, 73, 111].
Применение функционально-градиентных термопар позволяет увеличить КПД термопарного элемента по сравнению с однородными термопарами из таких же материалов ориентировочно на 10-25%.
