
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПНЕВМАТИЧЕСКИХ КОНСТРУКЦИЙ С ИСПОЛЬЗОВАНИЕМ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Численные методы [14—17]. В статье рассматриваются вопросы системного проектирования, разработки конструктивных решений и расчета легких и пневматических конструкций с общих позиций расчетчика, использующего численные методы, и проектировщика-конструктора.
Если еще в недавнем прошлом системное проектирование пневматических конструкций выполнялось архитекторами, анализ их формы — специалистами по моделированию, расчет конструктивных элементов—инженерами-конструкторами, а некоторые статические расчеты — специалистами по оболочкам, то сейчас все перечисленные задачи может самостоятельно решить любой из этих специалистов, используя современную программу численного расчета и вычислительное устройство размером с обычный микрокалькулятор. Разработка такого рода программы, получившей название РАМ —LISA по начальным буквам английских слов Programs in Advanced Mechanics — Lightweight Structures Analysis (программы в современной механике — расчет легких конструкций), изложена в данной статье. Есть все основания надеяться на значительный эффект, который может быть достигнут благодаря унификации методов расчета и проектирования, преодолению узкой специализации разработчиков конструкций и использованию поистине неограниченных возможностей современной вычислительной техники.
Использование современных вычислительных программ в значительной степени сводится к набору стереотипных операций, и поэтому при некотором навыке вполне доступно любому, кто доста точно хорошо представляет себе рассчитываемую конструкцию в ее физическом и инженерном аспектах. Работа с программой строится на интуитивной основе, подобно работе физика-экспериментатора или мастера-модельщика, и не имеет ничего общего с подходом математика, пользующегося аналитическими методами. Специалист, работающий с программой, может получить результат своей работы сразу в законченном виде и к тому же значительно быстрее, чем при использовании громоздких формул, утомительных выкладок и бесконечного ручного счета.
В статье не рассматриваются способы составления программ и преобразования физических зависимостей в численные алгоритмы. Машинные языки и алгоритмы — забота разработчиков программ, а не их пользователей, которым адресована эта статья.
Пневматические конструкции [1—3, 9—13, 24]. Эти конструкции обычно представляют собой мягкие (тканевые) оболочки, характеризующиеся пренебрежимо малой изгибной жесткостью. Несущая способность пневмооболочек может быть повышена наложением на них усиливающих канатов или тросовых сеток. Поэтому в качестве основных составных частей пневмооболочек при их машинном расчете рассматриваются элементы собственно оболочки (мембранные элементы) и тросовые элементы. Стабильность формы пневматических конструкций обеспечивается внутренним давлением, вызывающим в воздухонепроницаемой оболочке (мембране) растягивающие усилия, которые воспринимаются самой оболочкой или передаются ею на несущую систему следующего уровня в структурной иерархии конструкции.
Воздухоопорные пневматические сооружения — это типичные оболочки низкого давления; постоянное внутреннее давление в них измеряется несколькими сантиметрами водяного столба. Трубчатые элементы пневмокаркасных сооружений и автомобильные шины — примеры оболочек высокого давления, измеряемого несколькими атмосферами. Мембраны и оболочки под гидростатической нагрузкой можно также рассматривать как своего рода пневматические оболочки, нагруженные нормальным давлением, переменным по поверхности. Существует еще целый мир биологических пневматических конструкций, рассмотрение которого, однако, выходит за рамки данной статьи, посвященной исключительно техническим пневматическим оболочкам.
Методика расчета [13, 20—22]. Методика расчета мягких оболочек (мембран), имеющая целью отыскание формы оболочки, ее раскрой и определение усилий, была разработана в связи с составлением машинной программы РАМ—LISA. Однако эта методика в достаточной етепени универсальна и не связана непосредственно с численным методом расчета, для которого она была первоначально использована. Та же самая методика может быть реализована, например, и при чисто эмпирическом подходе к расчету, хотя и в этом случае некоторые из необходимых этапов расчета легче выполнять численным методом. Вряд ли требуется лучщее доказательство гибкости численных методов расчета и их независимости от применяемых технических средств, чем очевидная взаимозаменяемость их с «физическими» методами. Это наглядно демонстрирует подлинную эффективность современных численных методов и служит достаточным вознаграждением для разработчиков программ за их нередко каторжный труд.
Метод конечных элементов. При использовании метода конечных элементов (МКЭ) конструкция надлежащим образом расчленяется на множество элементарных структурных единиц, реакции которых на приложенные к ним деформации и усилия могут быть запрограммированы для автоматизированного расчета на ЭВМ. Структурная единица (конечный элемент) может представлять собой прямолинейный отрезок троса (тросовый элемент), четырехугольный участок мембраны (мембранный элемент), недеформированный отрезок балки (балочный элемент), кубик в объеме массивной конструкции («блочный» элемент) и т. п. в зависимости от типа рассчитываемой конструкции.
После того, как реальная конструкция представлена расчетчиком в виде ансамбля (сетки) таких элементов, ЭВМ рассчитывает характеристики жесткости всех элементов и действующие в них усилия, объединяя полученные данные в систему уравнений равновесия в узлах (точках пересечения элементов). В результате рвения этой системы на ЭВМ определяют перемещения узлов, по которым в соответствии с программой рассчитывают деформации и напряжения в каждом из конечных элементов.
Если условие равновесия конструкции зависит от ее деформированной формы (т. е. конструкция является геометрически нелинейной), что характерно, за малым исключением, для всех легких конструкций, то решение выполняют путем итераций, причем на каждом шаге расчета определяют новое очертание конструкции, служащее основой для последующего шага итерационного процесса. Реализация МКЭ автоматизирована в такой степени, что для его успешного применения не требуется подробное знание функциональных аспектов метода. Это дает проектировщику возможность создавать конструкцию, используя данный метод интуитивно и чисто эмпирически, и требует от него почти исключительно лишь физического понимания технических аспектов формы конструкции и ее поведения под нагрузкой.
Программа для ЭВМ [21]. Приведенные в этой статье примеры конструктивных форм рассчитаны по машинной программе РАМ — LISA, использующей МКЭ для решения статических и динамических задач, либо по более раннему варианту этой программы (под названием MASL). Программа разрабатывалась автором начиная с 1969 г. сначала в Калифорнийском университете в Беркли (США) под руководством проф. Пауэлла, затем в Париже, потом в Эссене; в институте проф. Бубнера (совместно с Эльберманом) и снова в Париже в фирме «Инджиниринг систем интернэшнел».
Задачи проектирования. Проблема проектирования зданий и сооружений является комплексной и требует объединения усилий специалистов различных дисциплин. Архитектурное проектирование оперирует с такими категориями, как система, форма, функция, красота, влияние среды, технология, человеческие потребности, природа; Инженерное проектирование имеет дело с конструктивными системами, материалами, конструктивными размерами и элементами, внешними воздействиями. В инженерном расчете учитываются нагрузки, деформации и напряжения, вибрации, разрушения, надежность. , Существует мнение, что взаимосвязь архитектурного и инженерного проектирования является недостаточно тесной или вообще отсутствует. Более парадоксально, что недостаточна также взаимосвязь инженерного проектирования и инженерного расчета. Дело обстоит таким образом, что результаты инженерного расчета редко приводят к пересмотру концепций, принятых при инженерном проектировании, а соображения инженерного проектирования зачастую вообще не учитываются в архитектурных решениях. Такого положения не должно быть при создании легких конструкций, поскольку здесь существует по меньшей мере взаимозависимость между конструктивной системой и формой, между конструктивным решением и размерами конструкции, между нагрузками и деформациями. В этом смысле проблема проектирования легких конструкций может быть решена только на стыке различных дисциплин.
В настоящей статье рассматриваются инженерный расчет и системное проектирование легких конструкций. Здесь под инженерным расчетом подразумеваются отыскание точной формы конструкции и ее расчет на действующие нагрузки; при этом задача отыскания формы конструкции является для инженера-проектировщика новой и в то же время наиболее сложной. Обе проблемы могут быть решены на основе либо физического, либо численного эксперимента, т. е. с применением численного метода, как показано ниже.
Тросовые системы (рис. 1—7). Вопросы расчета тросовых систем освещены в работах [1, 4—8]. При использовании МКЭ тросовая система (рис. 1,а) предполагается состоящей из тросовых элементов (рис. 1,6). Простейший линейно-упругий прямолинейный тросовый элемент имеет две узловые точки и характеризуется своей начальной длиной L0, модулем упругости Е и площадью поперечного сечения А. Тросовая система образуется из элементов, соединенных между собой в узловых точках, которыми являются точки пересечения тросов или промежуточные точки отдельного криволинейного свободно висящего троса (рис. 1, в). Каждый тросовый элемент передает от узла к узлу растягивающее усилие; если элемент может передавать также сжимающее усилие, его называют стержневым элементом (рис. 1, г).
При линейно-упругом материале растягивающее (сжимающее) усилие в элементе пропорционально изменению его длины (рис. 2, а). Возможен также учет нелинейно-упругих, пластических и вязкоупругих (зависящих от времени) деформаций материала (рис. 2, б—г).

Для расчета формы перекрестных тросовых систем (сеток) необходимо введение напрягающих или стабилизирующих, тросовых элементов (рис. 3,а). Физически каждый из таких элементов подобен тросу, перекинутому через вращающийся без трения блок и натянутому грузами постоянного веса. При численном расчете напрягающий элемент, соединяющий два узла, характеризуется отсутствием сопротивления продольным деформациям и заданным значением (положительным или отрицательным) передаваемого им усилия.
Возможно также использование так называемых гравитационных элементов (рис. 3,6), т. е. тросовых элементов, усилия в которых обратно пропорциональны квадрату их длины и прямо пропорциональны произведению связанных ими масс (рис. 2, д). Благодаря этому можно распространить область применения программы расчета тросовых систем на расчеты движения небесных тел.
При необходимости могут быть использованы и тросовые элементы более общего вида, обладающие заданными характеристиками собственного веса, массы, изменения свойств при температурных воздействиях, регулируемой длины, предварительного напряжения, лобового сопротивления (при движении в вязких средах, воде, воздухе), внутреннего трения, разрушения и т.п. (рис.4).
Включение в программу расчета всех перечисленных вариантов позволяет решать весьма широкий круг задач с использованием одного и того же расчетного аппарата. В качестве примеров можно привести выполненные по разработанным автором программам расчеты модели вантового покрытия института Ф. Отто в Вайхингене (рис. 5), висячего тросового покрытия с шестиугольными ячейками (рис. 6), трансформируемого сетчатого покрытия (рис. 7); эти работы были выполнены в Беркли (США) в 1969 г. Модифицированный вариант программы был использован для расчета колебаний длинных якорных тросов при волновом воздействии и для расчета движения системы двух искусственных спутников Земли, связанных тросом; эти работы выполнены в Париже в 1975 и 1979 гг.


Мягкие оболочки (рис. 8-24). Расчет таких конструкций подробно рассмотрен в работах [I, 2, 9—13, 18, 19]. При расчете с привлечением МКЭ оболочка расчленяется на конечные мембранные элементы в форме треугольников, четырехугольников или многоугольников.
Четырехугольный мембранный элемент (рис. 8, а) геометрически определяется четырьмя своими узловыми точками (в углах) и толщиной оболочки; срединная поверхность элемента принимается в форме гиперболического параболоида. Материал элемента предполагается состоящим из изотропной матрицы и ряда армирующих слоев (до четырех) из упругих волокон различного направления (рис. 8,6). Мембранные элементы могут характеризоваться собственным весом (рис. 8,в), заданной временной нагрузкой (рис. 8,г), массой (рис. 8,(3), нормальным равномерно распределенным (рис. 8, е) или гидростатическим давлением, изменением свойств при температурных воздействиях (рис. 8,ж) и т.п.
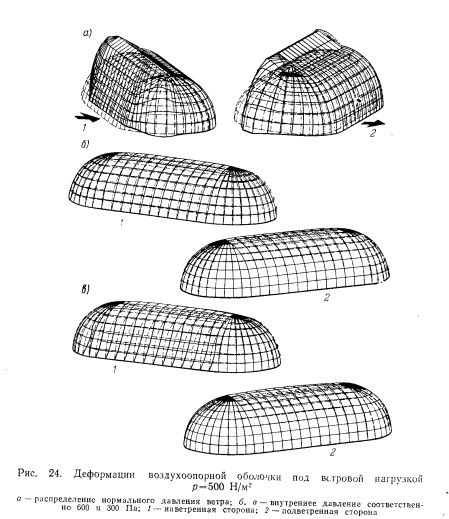
Мягкие оболочки в общем работают аналогично тросовым системам, но в отличие от них обладают сопротивлением сдвигу, как и пленки и ткани, из которых они выполнены. Мягкие оболочки хможно подразделить на предварительно напряженные (тентовые), надувные (пневматические) и оболочки, нагруженные гидростатическим давлением. В последние годы численный метод был широко использован для расчета форм различных мягких оболочек — изотропных (рис. 9—15) и анизотропных (рис. 16), мыльных пленок, контейнеров (рис. 17), плавучих оболочек (рис. 18), оболочек с усилением тросовыми сетками (рис. 9, в), автомобильных шин, мягких переборок (рис. 19), плотин (рис. 20) и воздухоопорных сооружений (рис. 21—24). Эти работы были выполнены автором в 1970—1979 гг. в Беркли (США), Штутгарте, Париже и Эссене (совместно с Эльберманом). Приведенные примеры характеризуют широкие возможности программы MASL, разработанной для расчета тросовых систем и мягких оболочек.

Процедура отыскания формы мягких оболочек достаточно сложна, поскольку необходимо учитывать сопротивление материала оболочки сдвигу. Что же касается характера нагрузок на мягкие оболочки, то он, по-видимому, не вносит в расчет дополнительных трудностей по сравнению с тросовыми системами. Поэтому мы остановимся лишь на особенностях процедуры отыскания формы оболочек.
Отыскание формы мягких оболочек. В природе существуют физически реальные (хотя и эфемерные) формы мягких оболочек, обладающие замечательным свойством сохранять постоянное и равномерное натяжение в любой точке и во всех направлениях: это мыльные пленки. Мыльная пленка образует в то же время минимальную поверхность. Поэтому форму мыльной пленки часто используют в качестве исходной при проектировании мягких оболочек.

Конечные элементы, обладающие свойствами мыльной пленки (пленочные элементы), играют ту же роль при расчете мягких оболочек, что и тросовые элементы при расчете тросовых систем. Они характеризуются свойством сохранять изотропное натяжение, независимо от их деформированного состояния. Мягкую оболочку, образованную из таких пленочных элементов, можно рассматривать как идеализированную («чистую») форму, равновесное состояние которой однозначно определяется заданными напряжениями и внешними нагрузками.

Реальные мягкие оболочки в большинстве случаев изготовляют из ортотропных материалов, обладающих различной прочностью и жесткостью в двух взаимно перпендикулярных направлениях (соответствующих ориентации армирующих волокон). При этом «чистой» форме оболочки более соответствовала бы форма мыльной пленки с неравномерным распределением натяжений. Хотя в природе таких анизотропных «мыльных пленок» и не существует, они могут быть смоделированы численно, например, наложением на оболочку из изотропных пленочных элементов сетки напрягающих тросов (рис. 16). Таким образом можно численно рассчитать форму оболочки с заданным анизотропным напряженным состоянием.


Методика нахождения раскроя мягких оболочек на основе форм мыльных пленок (рис. 25) рассмотрена в следующем разделе.
Методика проектирования мягких оболочек [13, 20J. Раскрой мягкой оболочки представляет собой набор плоских ненапряженных сегментов, вырезанных из реального материала оболочки (см. рис. 25). Геометрия раскроя должна удовлетворять условию наилучшего приближения к заданным форме и напряженному состоянию оболочки после соединения ее элементов и приведения оболочки в проектное положение. Из практических соображений обычно наиболее удобен раскрой в виде длинных прямолинейных полос материала (рис. 25, в). Ниже на примере пневматической оболочки излагается последовательность этапов численного расчета оптимального раскроя.

Этап 1. Нахождение формы (рис. 26, а). Рассчитывают идеализированную («чистую») форму обрлочки с использованием изотропных или анизотропных пленочных элементов при наличии или отсутствии внутреннего давления. Например, при жестком прямоугольном контуре «чистая» форма оболочки образуется раздуванием первоначально плоской сетки пленочных элементов.
Этап 2. Замена напряженных элементов (рис. 26,6). Каждый из пленочных элементов в найденной «чистой» форме оболочки заменяют упругим мембранным элементом таким образом, чтобы он занимал то же положение в пространстве и имел то же напряженное состояние,. Это означает, что каждый заменяющий упругий мембранный элемент должен иметь в исходном состоянии меньшие размеры, чем соответствующий пленочный элемент; заданное напряженное состояние; элемента достигается благодаря растяжению материала. Определение «редуцированных» размеров элементов осуществляют автоматически по программе.

Этап 3. Выбор схемы раскроя (рис. 26, в). Задают принципиальную схему раскроя оболочки, например, в виде набора полос, причем ширину их принимают кратной размеру конечного элемента. Если полосы раскроя ориентированы вдоль геодезических линий поверхности «чистой» формы оболочки (так называемый геодезический раскрой), то их развертка на плоскость оказываемся наиболее близкой к прямолинейной. Сетку узловых точек пленочных элементов на поверхности «чистой» формы оболочки можно легко приблизить к геодезической путем наложения на нее минимальной сетки напрягающих тросов с одинаковым натяжением. Усилия в этих «вспомогательных» тросах могут быть весьма невелики, поскольку в реальных мыльных пленках частицы жидкости свободно перемещаются по поверхности, не испытывая сопротивления материала; это свойство учитывается и численной моделью.
Этап 4. Раскрой полотнищ (рис. 26,г). Полотнища материала, соответствующие принятой схеме раскроя, вырезают из находящейся в напряженном состоянии оболочки; при этом напряжения в них снимаются. В свободном от напряжений состоянии эти элементы оболочки принимают форму сегментов двоякой кривизны.
Этап 5. «Уплощение» выкройки (рис. 26, д). Свободные от напряжений сегменты развертывают на плоскость таким образом, чтобы работа необходимой для этого деформации материала была минимальной. Такая развертка соответствует наименее стесненной плоской форме элементов раскроя, при которой в них появляются минимальные самоуравновешенные напряжения, тогда как в идеальном случае материал должен быть вообще; свободен от напряжений.
Этап 6. Окончательный раскрой (рис. 26, е). Окончательный раскрой оболочки осуществляют путем разрезки материала оболочки (без натяжения) на полосы, форма которых точно соответствует очертанию развертки сегментов оболочки на плоскость.
Этап 7. Возведение (рис. 26,ж). Проектную форму оболочки находят путем соединения элементов окончательного раскроя и приложения к ним всех действующих нагрузок (усилий). Оболочка в проектном положении будет иметь в общем то же напряженное состояние, что и ее «чистая» форма; дополнительные напряжения примерно соответствуют напряжениям, возникающим при развертке; криволинейных сегментов оболочки на плоскость, но с обратным знаком. Эти дополнительные напряжения вызываются деформациями, необходимыми для придания двоякой кривизны первоначально плоским элементам раскроя оболочки. В силу сопротивления элементов раскроя этим деформациям проектная форма оболочки также будет несколько отличаться от «чистой» формы. Однако при использовании описанной выше процедуры расчета указанные неизбежные отклонения формы и напряженного состояния оболочки от первоначально заданных оказываются в среднем минимальными.

Модель технической ткани [21—27] (рис. 27—34). Одной из наименее, разработанных задач, связанных с расчетом мягких оболочек, является точное численное описание свойств тканевых материалов с покрытиями (рис. 27). Решение этой задачи особенно важно в связи с применением все более жестких и прочных тканей (композиций типа «кевлар» и «майлар», стеклотканей с покрытием тефлоном и т.п.) и с требованием снижения веса конструкций при одновременном повышении уровня действующих в них напряжений. Поэтому ниже подробно рассмотрена наглядная техническая модель тканевого материала с покрытием, которая может быть также использована в качестве основы для построения более совершенных моделей, отличаясь простотой концепции и удачной формой прямого описания достаточно сложного объекта.

На микрофотографиях образца типичной ткани полотняного переплетения с покрытием можно увидеть начальное волнообразное искривление нитей основы и утка и их постепенное выпрямление при растяжении образца. Первоначальное сопротивление образца растяжению обусловлено хотя и малой, но сказывающейся при столь небольших расстояниях изгибной жесткостью нагруженных нитей и нитей перпендикулярного направления, кривизна которых при нагружении образца возрастает. Эффективная изгибная жесткость нитей еще увеличивается благодаря наличию полимерного покрытия, в массе которого они заключены.
В силу сказанного диаграммы «напряжение — деформация» при одноосном растяжении ткани (рис. 28) заметно нелинейны, причем в начальной стадии нагружения, когда происходит выпрямление нагруженных волокон, сопротивление ткани невелико, а в дальнейшем ее жесткость и сопротивление возрастают, поскольку эти волокна уже полностью вытянуты. Таким образом, кинематическое взаимодействие нитей основы и утка обусловливает начальную нелинейность деформирования ткани, даже если материал волокон предполагается линейно-упругим или нерастяжимым.
Другая основная причина нелинейности деформирования ткани заключается в нелинейной зависимости между напряжениями и деформациями, характерной для некоторых типов волокон, из которых изготовлены нити ткани (рис. 29). Например, полиэфирные волокна имеют значительную жесткость при малых деформациях, затем их жесткость резко снижается и вновь возрастает при высоких деформациях.
Оба фактора, обусловливающих нелинейный характер деформаций ткани с покрытием, могут быть достаточно просто учтены в расчете, если использовать для численного описания одноосной и двухосной деформации материала нелинейную стержневую модель, соответствующую типичному многократно повторяющемуся узлу пересечения нитей основы и утка. Эта модель использована для автоматического определения параметров мембранных конечных элементов в рамках машинной программы расчета РАМ — LISA (рис. 30).
В точках сопряжения конечных элементов нити основы и утка заменяются нелинейными стержневыми элементами с начальными искривлениями, соответствующими начальным искривлениям нитей (рис. 31). В узел пересечения нитей вводится короткий стержневой элемент, расположенный перпендикулярно срединной поверхности ткани; таким образом фиксируется расстояние между стержнями, моделирующими пересекающиеся нити, и обеспечивается их кинематическое взаимодействие (рис. 32). Сдвиговая жесткость ткани с покрытием, определяемая в основном малым по величине сопротивлением сдвигу материала покрытия, моделируется в расчете непосредственно введением ортотропных напряжений сдвига в плоскости мембраны, задаваемых как характеристики материала.
В машинной программе расчета описанная модель используется путем замены сплошного материала мембраны структурой, состоящей из соединенных между собой нелинейных стержневых элементов (рис. 31, в). При этом реакция мембранного элемента, например, на приложенные к нему деформации определяется в результате последовательных итераций из условия равновесия всех узлов стержневой модели.
Отдельные нелинейные стержневые элементы в описанной модели могут характеризоваться линейными или нелинейными свойствами материала. В простейшем случае можно принять, что материал деформируется линейно-упруго при изгибе и при осевом растяжении. Стержневым элементам можно также приписать свойство нелинейной растяжимости в осевом направлении, характеризуемой криволинейной диаграммой «напряжение—деформация»,в том числе и с линейной разгрузкой (рис. 29), что соответствует линейному или нелинейному поведению отдельных типов волокон. Далее, поперечные стержневые элементы, которые фиксируют расстояние между стержнями, моделирующими нити основы и утка, могут обладать продольной упругостью, что позволяет моделировать упругие контактные деформации нитей в местах их пересечения при двухосном натяжении ткани. Наделяя поперечные стержни упруго-пластическими свойствами, можно частично воспроизвести эффект остаточного поперечного обжатия, характерный для большинства технических тканей, особенно на первых циклах истории нагружения.
Описанная модель, очевидно, может быть еще уточнена с учетом вязкоупругих свойств (ползучести) материала и т.д., но и в существующем виде она оказалась исключительно полезной при решении весьма ответственных практических задач. На рис. 33 и 34 приведены кривые «напряжение — деформация» для некоторых технических тканей, полученные опытным путем и рассчитанные с использованием описанной модели; сравнение этих кривых свидетельствует о высокой точности модельного описания свойств материала. Параметры стержневой модели (ее геометрия, осевые и изгибные жесткости стержней) могут быть разумным образом рассчитаны из условия наилучшего приближения к опытным кривым (такой расчет быстро сходится после нескольких попыток), причем геометрические параметры стержневой модели можно определить и непосредственно по геометрии переплетения ткани.
Пневмобалки [28] (рис. 35—36). По программе РАМ—LISA был произведен расчет пневмобалки с отношением диаметра сечения к длине 1:10 для простейших видов нагружения, давший хорошую сходимость с результатами лабораторных испытаний на модели. Было рассмотрено четыре вида нагружения - внутреннее избыточное давление в сочетании с осевым сжатием, изгибом, поперечным сдвигом и кручением. Вследствие значительных перемещений и деформаций пневмобалки результаты расчета для трех последних видов нагружения различались в зависимости от того, имелась или отсутствовала свободная деформация балки в осевом направлении. На рис. 35 в масштабе показаны деформированные состояния конечно-элементной модели пневмобалки при «чистом» изгибе (рис. 35, а), поперечном сдвиге (рис. 35,6) и кручении (рис. 35, в). На рис. 36 видно хорошее совпадение расчетных и экспериментальных результатов при «чистом» изгибе балки. Более широкая петля гистерезиса, полученная при лабораторных испытаниях, связана с трением в опорных узлах, которое не учитывалось в расчете.
Для расчета на ЭВМ использовали модель, состоящую примерно из 300 мембранных элементов. Модельные пневмобалки были изготовлены из коммерческой полиамидной ткани с неопреновым покрытием. Возможность местной потери устойчивости (складкообразования) оболочки пневмобалки вблизи ее торцов автоматически учитывалась программой расчета, причем ме;ста появления складок можно наблюдать на деформированной сетке конечных элементов, как показано на рис. 35,6. Однако геометрическая форма складок при этом не всегда воспроизводится, поскольку складка может локализоваться в пределах одного конечного элемента, который, по определению, не воспринимает сжимающих усилий в любом направлении.
Аэростат «Венера» [22] (рис. 37). Французским Национальным центром космических исследований были проведены опытные работы по проектированию газонаполненного аэростата, предназначенного для спуска в атмосферу планеты Венера. Аэростат представляет собой сферу диаметром около 9 м и объемом около 400 м3 с тонкой легкой оболочкой сложной структуры, состоящей из высокопрочной ткани с многослойным покрытием, которое включает отражающие и защитные слои. Для расчета оболочки была использована программа РАМ-LISA.
В соответствии с программой совместных советско-французских космических исследований аэростат должен быть изготовлен во Франции и доставлен советским космическим кораблем на орбиту, описываемую вокруг Венеры. При отделении от корабля-носителя аэростат должен быть заполнен газом под давлением около 50 мбар (5 кПа), чтобы на орбите нести научное оборудование массой около 250 кг. Общая масса аэростата с грузом составляет около 370 кг, из них масса оболочки — около 75 кг. Градиент избыточного давления газа в оболочке и давления в атмосфере Венеры на расчетной высоте орбиты составляет около 8-10-9 Н/мм3, что обеспечивает подъемную силу, необходимую, чтобы уравновесить силу тяжести при расчетной массе аэростата с грузом, создаваемую притяжением Венеры на высоте орбиты.

Оболочка аэростата (см. рис. 37, а) выполнена из 32 одинаковых сегментов меридиональной разрезки, соединенных наклеенными на них полосами ткани шириной 5 см, которые проходят от одного полюса оболочки к другому. Эти полосы изготовлены из того же материала, что и оболочка, но с таким расчетом, чтобы они не упрочняли оболочку в меридиональном направлении. Высокопрочная ткань оболочки (из волокна типа «кевлар», «майлар» и т.п.) выполнена таким образом, что ее нормальные характеристики (диаграммы деформирования при одноосном растяжении) в направлении основы и утка (см. рис. 33) почти не отличаются, т. е. ткань имеет практически одинаковую деформативность и прочность в двух взаимно перпендикулярных направлениях. Этого обычно не бывает у большинства коммерческих тканей, которые отличаются меньшей деформативностью в направлении основы, поскольку нити основы первоначально менее искривлены, чем уточные (см. рис. 34). На полюсах оболочки имеются жесткие металлические диски диаметром 0,7 и 1 м, служащие для крепления меридиональных сегментов оболочки.
В задачи расчета входило:
нахождение «чистой» формы оболочки, соответствующей напряженному состоянию равномерного растяжения;
построение реальной формы оболочки из материала с заданными характеристиками, соответствующего «чистой» форме с минимальными отклонениями от нее по геометрии и напряженному состоянию;
исследование напряженного состояния и деформаций оболочки при различных нагрузках.
При этом использована методика, изложенная в разделе «Методика проектирования мягких оболочек», за исключением этапа 3 (выбор схемы раскроя), поскольку заранее задан геодезический раскрой оболочки в виде меридиональных сегментов.
В силу симметрии каждого из 32 сегментов оболочки при расчете моделировался только один полусегмент; его конечно-элементная модель состоит из 732 мембранных элементов: 176 элементов по длине меридиана и 4—5 элементов по ширине полусегмента (рис. 38). Металлические диски у полюсов оболочки моделировались жесткими конечными элементами.

На этапе 1 отыскивается «чистая» форма оболочки (т. е. форма эквивалентной мыльной пленки) при совместном действии внутреннего давления, линейно изменяющегося атмосферного давления, полезного груза н постоянной нагрузки от полярных дисков, из условия, чтобы объем аэростата (с учетом деформаций оболочки) был в точности равен объему, необходимому для плавания аэростата в атмосфере Венеры на строго определенной высоте. Эта «чистая» форма показана на рис. 37, б и в; суммарное значение растягивающих усилий в оболочке составляет около 10,8 Н/мм.
На этапе 2 по программе автоматически выполняется замена всех 732 пленочных элементов на соответствующие им по положению в пространстве элементы нелинейно-упругого тканевого материала с покрытием, имеющие заданное натяжение 10,8 Н/мм.
Таким образом, заменяющая мембрана имеет ту же форму и то же напряженное состояние, что и исходная «мыльная пленка». Такое соответствие, вообще говоря, не будет достигнуто, если не проводить расчет строго по этапам 1 и 2 разработанной методики. Например, на рис. 39 показаны боковой вид и разрез оболочки аэростата (в исходном состоянии) при раскрое ее просто по идеальной сферической поверхности; при наполнении газом оболочка увеличивается в размерах, а усилия от подвешенного полезного груза искажают ее напряженное состояние, как показано на рис. 40,6.
На этапе 4 осуществляется «разгрузка» оболочки, и элементы раскроя ткани, благодаря ее упругой редеформации, принимают форму сегментов двоякой кривизны, свободных от напряжений. Далее в специальном блоке программы производится развертка этих сегментов на плоскость (этап 5). При этом в материале оболочки возникают минимальные «паразитические» внутренние напряжения, непревышающие ±30 % расчетного напряжения, равного 10,8 Н/мм; наибольшего значения они достигают в меридиональном направлении, вблизи экватора оболочки. Эти «паразитические» напряжения связаны с упругим деформированием сегментов двоякой кривизны при их развертывании на плоскость, причем значения напряжений зависят от размеров элементов раскроя и от деформативности ткани. Окончательный раскрой оболочки получают на этапе 6 в виде набора плоских сегментов материала, очертание которых в ненапряженном состоянии строго соответствует очертанию развертки сегментов оболочки на плоскость.
Заключительный блок программы расчета (этап 7) предусматривает соединение элементов окончательного раскроя оболочки между собой и приложение к ним начального внутреннего давления, а также всех нагрузок, ранее учтенных при нахождении «чистой» формы оболочки (наделенной свойствами мыльной пленки). При нагружении первоначально плоские элементы раскроя принимают форму сегментов двоякой кривизны, в связи с чем в оболочке появляются неизбежные, но минимальные «паразитические» напряжения, достигающие ±30 % среднего значения расчетного равномерного натяжения оболочки, равного примерно 10,8 Н/мм. Наибольшие «паразитические» напряжения развиваются вблизи экватора оболочки. Реальная форма оболочки, рассчитанная по описанной методике, незначительно отличается от исходной «чистой» формы, что видно на поперечном разрезе оболочки (см. рис. 37, г).

Эффективность разработанной методики проектирования пневмооболочек иллюстрируется картинами изостат меридиональных натяжений вблизи нижнего полюса оболочки аэростата при ее раскрое соответственно строго по разработанной программе (см. рис. 40, а) и просто по сферической поверхности (см. рис. 40,6). При «сферическом» раскрое меридиональные натяжения достигают значения 21,5 Н/мм, тогда как в правильно запроектированной оболочке эти натяжения оказываются весьма близкими к расчетному значению, равному 10,8 Н/мм.
Специально было исследовано напряженное состояние оболочки аэростата при возможных систематических отклонениях по ширине элементов раскроя. Для этого были заданы отклонения от номинальной ширины в форме синусоиды с амплитудой 0,3 мм и длиной волны около 200 мм при их наиболее неблагоприятном расположении (вблизи верхнего полюса оболочки). В результате максимальные упругие натяжения в кольцевом направлении достигали 27 Н/мм (см. рис. 40, в), т. е. значительно превосходили расчетное значение натяжения, равное 10,8 Н/мм. Отсюда следует, что при использовании современных жестких и высокопрочных тканей особо важное значение имеет обеспечение высокой точности расчета и исполнения раскроя оболочки.
Заключение. В настоящей статье предпринята попытка показать подход к проектированию и расчету пневматических конструкций на основе применения современных численных методов. Используемая для этих целей программа РАМ—LISA позволяет полностью осуществить проектирование легких конструкций, начиная с нахождения формы оболочки, обладающей свойствами мыльной пленки, до построения точного раскроя оболочки и расчета усилий в ней от действующих нагрузок. Особое внимание уделено общей методике проектирования мягких оболочек (мембран), обеспечивающей получение оптимальных конструктивных решений и представляющей собой универсальное рациональное средство для решения исключительно сложной задачи раскроя оболочек. Доступность и эффективность разработанной методики продемонстрированы на двух примерах из областей промышленной и космической техники.
Следует полагать, что предлагаемая методика является как раз тем необходимым звеном, которое может обеспечить решение проблемы рационального, эффективного и широкого применения современных высокотехнологичных материалов при инженерном и архитектурном проектировании долговечных пневматических и тентовых конструкций.
СПИСОК ЛИТЕРАТУРЫ
1. Otto F., Schleyer F. К. Zugbeanspruchte Konstruktionen, Band 2, Ullstein rachverlatj. Berlin, 1966.
2. Ishii K. On developing of curved surfaces of pneumatic structures. IASS Internationa! Symposium on Pneumatic Structures, Department of Architecture, Delft University of Technology. Delft, 1972.
3. Haug E. Powell, G. H. Finite Element Analysis of Nonlinear Membrane Structures. Structural Engineering Laboratory, University of California, Berkeley, California 1972.
4. Haug E. Berechnung von Seilfachwerken. IL Bericht 1/70, Mitteilungen des Instituts fur Ieichte Flachentragwerke (IL), Universitat Stuttgart, 1970.
5. Haug E. Berechnung von Seilnetzen. Teil 2. A priori Netze, IL Bericht 33/70, Mitteilungen des Instituts fiir Ieichte Flachentragwerke (IL), Universitat Stuttgart, 1970.
6. Haug E. Berechnung von Seilnetzen, Teil 3. A Method to define the Stress— Free Configuration of Prestressed Cable Nets. IL — Bericht 35/70, Mitteilungen des Instituts fiir Ieichte Flachentragwerke (IL), Universitat Stuttgart, 1970.
7. Haug E. Formermittlung von Netzen. Die Bautechnik, Heft 9, 1971, S. 294—299.
8. Haug E., Powell G. H. Analytical Shape Finding for Cable Nets. IASS Pacific Symposium — Part II on Tension Structures and Space Frame, Tokyo, October 1971.
9. Haug E., Powell G. H. Finite Element Analysis of Nonlinear Membrane Structures. IASS Pacific Symposium — Part II on Tension Structures and Space Frames, Tokyo, October 1971.
10. Haug E. Finite Element Analysis of Pneumatic Structures. IASS International Symposium on Pneumatic Structures, Department of Architecture, Delft University of Technology, Delft, 1972.
11. Haug E., Oelbermann J, Numerical Design and Analysis on Air Supported Structures IASS International Symposium on Air Supported Structures, Venice, 1977.
12. Haug, E., Oelbermann, J. Numerische Ermittlung von Minimalflachen, Symposium Minimalkonstruktionen, Essen, March 1977. R. Miillcr, Koln—Braunsfeld.
13. Oelbermann J., Haug, E. Berechnung des Zuschnitts einer Membrane mit Hilfe der Finiten Element Methode; 2nd International Symposium Weitgespannte Flachentragwerke, University of Stuttgart, May 14—18, 1979.
14. Oden J. Т., Bathe K. J. A Commentary on Computational Mechanics, Applied Mechanics Reviews, Vol. 31, No. 8, August 1978.
15. Roache P. J. Computational Fluid Dynamics (Introductory Chapter), Her- mosa Publishers, Alburquerque, N. M, 87108, 1976.
16. Wilson E. L. Automated Analysis and Design of Complex Structures, Paper Ml/1, 4th SMIRT Conference, San Francisco, 1977.
17. Duddeck H. Zu den Berechnungsmodellen der Technik. Die Bautechnik, Heft 10, October 1976.
18. Schwenkel D. Mathematisch numerische Methoden zur Approximation und Abbildung der Systemgeometrie weitgespannter Fiachentragwerke. Dissertation, IAGB Universitat Stuttgart, 1977, DGK, Reihe C, Nr. 243 und SFB 64 Mitteilungen 46/78.
19. Brinkmann G. Statische Berechnung von gleichmaschigen Netzen und Membranen auf spezieilen Flachen mit Hilfe der Vectoranalysis, SFB 64-Mitteilungen 42/76.
20. Haug E. Engineering Contributions to the Design of Lightweight Structures via Numerical Experiments, 2nd International Symposium Weitgespannte F1S- chentragwerke, University of Stuttgart, Vol. 2, May 1979.
21. Haug E. Program PAM—LISA, user's and theoretical manual, Engineering System International, 20 rue Saarinen, 94578 RUNGIS CEDEX, France September 1980.
22. Haug E., Winkelmuller G. Optimisation Nnmerique de la Forme du Ballon Venus, Rapport EE 79—641, Engineering System International, 20 rue Saarinen, 94578 RUNGIS CEDEX, France, June 1980.
23. Kawaguchi Y. et al. Engineering Problems of Pneumatic Structures, paper 5—6 of the IASS Pacific Symposium — Part II on Tension Structures and Space Frames, Tokyo, 1971.
24. Shimamura S. and Takeuchi O. Mechanical Behaviour of Selected Coated Fabrics used in Membrane Structures in Japan, paper 6—1 of the IASS Pacific Symposium — Part II on Tension Structures and Space Frames, Tokyo 1971.
25. Losch М. H. Bestimmung der Mechanischen Konstanten fiir einen zwei- dimensionalen, nichtlinearen, anisotropen, elastischen Stoff am Beispiel beschichteter Gewebe, Dissertation University of Stuttgart, Prof. U. Wegner, University of Stuttgart, 1971.
26. Reinhardt H. W. Ein und zweiachsige Verformungs und Festigkeitsunters- rechungen an einem beschichteten Gittergewebe, Mitteiiungen 31/1975. Sonder- forschungsbereich SFB 64, Otto-Graf-Institut, University of Stuttgart, 1975.
27. Meffert B. Mechanische Eigenschaften PVC — beschichteter Polyestergewebe, Institut fiir Kunststoff-verarbeitung (IKV), Technische Hochschule Aachen, Pontstr, 49, 5100 Aachen, Mai 1978.
28. Haug E., Winkelmuller G., Curnier A., de Rouvray A. ESI-Internal Report, Engineering System International, 20 rue Saarinen, 94578 Rungis Cedex, France, October 1980.
В. Ермолов, У. У. Бэрд, Э. Бубнер и др., Пневматические строительные конструкции, М., 1983
