
Основы теории подобия
Для того чтобы по данным лабораторных исследований прогнозировать с достаточной достоверностью соответствующие характеристики работы сооружения в натуре (например, значения скоростей потока в НБ, напряжений в теле плотины и др.), надо знать законы подобия, на основе которых проектируют модели и делают пересчет в натуру результатов опытов, полученных на модели.
Как следует из теории подобия, подобными называются явления, протекающие в геометрически подобных системах, в которых происходят процессы одинаковой физической природы и одноименные величины (линейные размеры, скорости течения и др.) имеют постоянное отношение междц собой [431.
В соответствии с этим для двух рассматриваемых систем (например для натуры и модели) должны быть постоянными масштабные коэффициенты (или константы подобия) а, то есть отношения соответствующих одноименных величин:
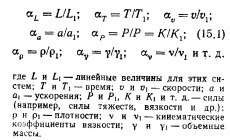
Рассмотрим механическое подобие систем, то есть случаи движения твердых тел или жидкости (покой — статические воздействия — частный случай). При этом различают подобие геометрическое, кинематическое и динамическое.
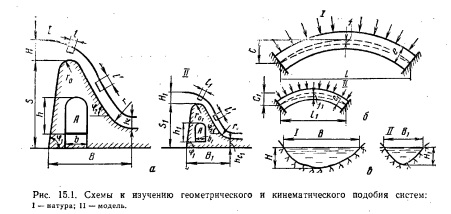
Геометрическое подобие. В соответствии с выражениями (15.1) геометрическое подобие будет выполнено, если для всех соответствующих линейных размеров двух рассматриваемых систем (далее будем считать их натурой и моделью) будет постоянным, то есть (рис. 15.1, а)
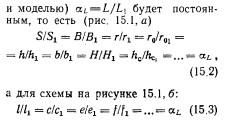
При соблюдении геометрического подобия формы модели и натуры должны быть подобны, то есть, например, углы должны быть одинаковы для обеих систем.
При моделировании требования геометрического подобия надо удовлетворять не формально, а с учетом того, какая задача рассматривается. Например, при гидравлических исследованиях водослива (рис. 15.1, а) нет необходимости на модели воспроизводить полость А в теле водослива [то есть нет необходимости в формуле (15.2) приводить отношения, а при исследованиях прочности конструкции воспроизвести такую полость нужно, если она не слишком мала. Если при гидравлических исследованиях указанного водослива определяют лишь его пропускную способность, то очень важно соблюсти геометрическое подобие оголовка и прилегающих к нему зон, но не важно (так как за оголовком бурный режим и форма носка не влияют); если же исследуется и концевая часть водослива, то нужно соблюсти условие геометрического подобия и для этой зоны.
При соблюдении геометрического подобия собственно модели не всегда можно получить геометрическое подобие для всех сходственных линейных размеров потока. Например, при может оказаться, что (рис. 15.1, а), если не промоделированы сопротивления на водосливной поверхности (шероховатость). Это надо иметь в виду.
При прочностных исследованиях (см. 15.1.4) различают строгое и нестрогое (приближенное) геометрическое подобие. В первом случае условие геометрического подобия соблюдается не только для генеральных размеров сооружения, но и для деформаций, то есть в зависимость (15.3) включено и отношение прогибов. Иначе говоря, ставится и условие:
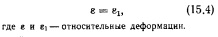
При исследовании напряженно-деформированного состояния сооружений в упругой стадии это условие часто не выполняется (см. 15.1.4), то есть принимается (так называемое «расширенное» подобие), что облегчает измерение деформаций. Последнее возможно лишь при условиях: 1) чтобы деформации не модели были достаточно малыми и существенно не влияли на генеральные размеры и форму сооружения (на моменты, продольные и поперечные силы); 2) не было бы потери устойчивости модели.
Если геометрическое подобие не соблюдено и исследуются модели с искажением масштаба, что часто принимают при изучении русловых процессов (см. 15.1.3), то моделирование будет приближенным. В этом случае будут разные константы подобия для глубины и ширины: (рис. 15.1, в).
Кинематическое подобие. Оно требует, чтобы соответствующие частицы обеих систем совершали геометрически подобные перемещения в промежутки времени, находящиеся в постоянном соотношении (рис. 15.1, а). Кинематическое подобие удовлетворяется, если соблюдены требования геометрического и динамического подобия.



Это условие используют, например, при изучении вибраций и напряженного состояния конструкций (работающих в упругой стадии) в потоках с высокой турбулентностью, для которых при гидравлическом моделировании основным будет критерий Фруда. Данное условие практически вполне выполнимо.
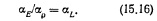
Допустим, что надо исследовать динамическую работу раздельной стенки, расположенной в НБ в зоне гидравлического прыжка. Пусть масштаб модели 1:25 (25). Примем то есть для модели надо применить материал с той же объемной массой, что и для натуры. В соответствии с (15.16) получаем 25. Если в натуре исследуемая стенка выполнена из бетона с модулем упругости 29,4 ГПа, то модель ее надо изготовить из низкомодульного тяжелого ( 2,4-103 Н/м3— как и для бетона) материала с модулем упругости. Такие материалы имеются (см. 15.4).
Установление критериев подобия из условия тождественности дифференциальных уравнений, описывающих рассматриваемый процесс. Подобные явления должны описываться аналогичными дифференциальными уравнениями; иметь подобные условия однозначности, в которые входят геометрические свойства системы (то есть должно быть выполнено геометрическое подобие), граничные и начальные условия, а также существенные физические константы и, кроме того, одинаковые критерии подобия, составленные из величин, входящих в условия однозначности.
При моделировании гидравлических явлений, если исходить из уравнений неустановившегося движения вязкой жидкости (уравнений Навье—Стокса) при их тождественности для модели и натуры, получим следующие безразмерные критерии [43]:
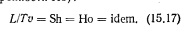
Это чисто кинематический критерий, появляющийся при неустановившемся движении жидкости. По своему смыслу он представляет просто безразмерный период (например, волн) или безразмерную частоту). Совершенно естественно, при рассмотрении действующих сил его не было и он не является частным случаем общего критерия Ньютона (15.8).
Критерия Вебера нет при рассмотрении подобия на основе уравнений Навье—Стокса, так как они не учитывают силы поверхностного натяжения, хотя в ряде случаев эти силы и оказывают некоторое влияние на течение.
Критериальные уравнения и автомодельность. Установив из .рассмотрения существа данного явления или из анализа дифференциальных уравнений, описывающих данный процесс, от каких безразмерных критериев подобия этот процесс зависит или может зависеть (определяющие критерии), следует найти соответствующую зависимость между этими критериями, которую называют критериальной зависимостью или критериальным уравнением. Вместо того, чтобы найти теоретическое решение соответствующих дифференциальных уравнений, что при сложных граничных условиях бывает весьма трудной и часто пока неразрешимой задачей, в данном случае критериальную зависимость решают экспериментально, путем моделирования.
Например, для неустановившегося движения вязкой жидкости, описываемого уравнениями Навье—Стокса, критериальное уравнение имеет вид:

Если в некоторой области тот или иной критерий перестает влиять на изучаемую величину, говорят, что наступила область автомодельности (в рассматриваемом случае — по Re). Тогда один из критериев выпадает из рассмотрения и моделирование упрощается. При гидравлическом моделировании (см. 15.1.3) это происходит при числах Рейнольдса, больших некоторых критических, или граничных, значений.
