ПОДОБИЕ НАСОСОВ
МОДЕЛИРОВАНИЕ НАСОСОВ
При проектировании НС и обосновании условий их эксплуатации необходимо иметь полную информацию об энергетических и кавитационных свойствах насосов в различных режимах их работы. Эта информация, получаемая экспериментально на модельных установках, представляется в форме характеристик насоса.

Моделирование насосов позволяет на основе подобия физических процессов, протекающих в проточном тракте модели, судить о свойствах натурного насоса. Однако для этого потребуется обеспечить гидродинамическое подобие натурного насоса с моделью, заключающееся в соблюдении условий геометрического, кинематического и динамического подобия.
Геометрическое подобие сводится к тому, что все элементы проточной части рассматриваемых насосов, включая шероховатость обтекаемой поверхности, геоме-трически подобны в соблюдении условий геометрического, кинематического и динамического подобия.
Геометрическое подобие сводится к тому, что все элементы проточной части рассматриваемых насосов, включая шероховатость обтекаемой поверхности, геоме-трически подобны.
Геометрически подобные насосы, различающиеся диаметром рабочего колеса Dlt образуют насосную серию.
Кинематическое подобие требует, чтобы в геометрически подобных точках потока насосов треугольники скоростей были подобны. Режимы работы насосов, в которых соблюдается кинематическое подобие, называются изогональными. Условия кинематического подобия могут быть записаны как:
Динамическое подобие означает пропорциональность всех действующих сил в геометрически подобных точках насосов при изогональных режимах. Если на поток в насосе действуют силы вязкости, тяжести, давления, инерции, то динамическое подобие обусловливается равенством чисел Рейнольдса, Фруда, Эйлера и Струхаля:
Между равенствами (9-15) должна существовать определенная зависимость, которую выразим критериальным уравнением:
При соблюдении для модельного и натурного насосов равенств чисел Re, Fr, St будет соблюдаться и равенство чисел Ей. Равенство чисел St для насосов может быть обеспечено путем установления соответствующих частот вращения роторов рассматриваемых гидромашин. При моделировании насосов одновременное соблюдение условий подобия по крите-риям Re и Fr невозможно. Необходимо установить, какие силы являются определяющими исследуемое явление, и обеспечить соблюдение одного из критериев. При изучении процес-сов в насосе, связанных с силами трения, достаточно соблюсти подобие чисел Re. Обычно на практике это не выполняется. Однако испытываемая модель и натурный насос работают в зонах автомодельности, в которых числа Re не оказывают существенного влияния на ха-рактеристики потока жидкости. Различие чисел Re и относительной шероховатости обте-каемых поверхностей модельного и натурного насоса требует необходимости пересчета результатов модельных исследований на натурные условия. Равенство чисел Фруда необ-ходимо соблюдать при исследовании блоков НС, имеющих свободную поверхность потока в нижнем и верхнем бьефах,
УРАВНЕНИЯ ПОДОБИЯ
Установим связь между напорами, подачами и мощностями двух насосов одной серии, работающих в изогональных режимах и различающихся диаметрами рабочего колеса и частотами вращения.
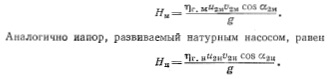

Напор, развиваемый модельным насосом, для условий безударного входа определим с учетом (9-10) как:
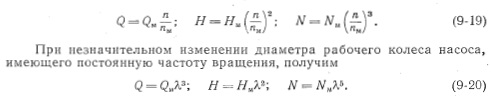
Аналогично напор, развиваемый натурным насосом, равен
Используя (9-12), (9-13), (9-14), можем записать отношение напоров рассматриваемых насосов:
Учитывая, что подача насоса изменяется пропорционально изменению площади выходного сечения рабочего колеса и радиальной составляющей скорости, используя (9-13) и (9-14), получим:
Принимая ри = рм и подставляя значение Q и Н из уравнений (9-16) и (9-17), получим отношение мощностей)
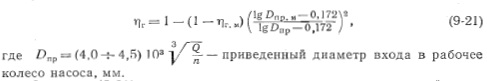
Уравнения (9-16) — (9-18) позволяют с большой точностью определить основные па-раметры натурного насоса, если известны параметры другого насоса данной серии. Они позволяют пересчитывать на натурные условия характеристики насосов, полученные на модельных установках.
Зависимость (8-4, а) справедлива и для насосов, если не учитывать изменение КПД насоса с изменением его диаметра.
Экспериментально установлено, что для одного и того же насоса при значительном изменении числа Re в области автомодельности, отношение составных частей КПД практически не меняется. Поэтому на основе формул (9-16) — (9-18), опуская индекс «н», запишем параметры насоса при изменении частоты вращения.
При незначительном изменении диаметра рабочего колеса насоса, имеющего постоянную частоту вращения, получим

Формулы (9-20) применяются для определения параметров центробежного насоса с подрезанным рабочим колесом.
Проблема обоснованного пересчета КПД насоса с модели на натуру еще окончательно не решена. Имеется ряд формул пересчета КПД, основанных на теоретических предпосылках и экспериментальных данных. В практике насосостроения используется полуэмпириче- ская формула А. А. Ломакина для пересчета гидравлического КПД центробежного насоса
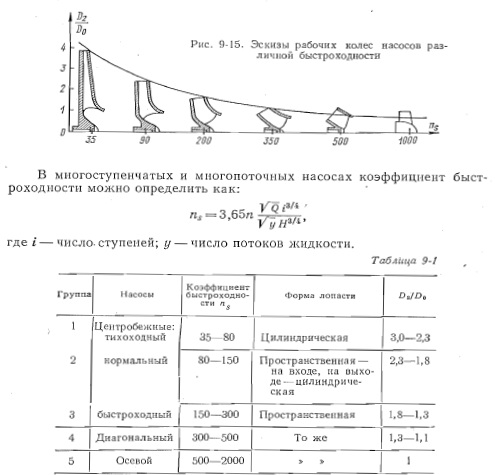
Коэффициент быстроходности одновременно учитывает три важных параметра насоса: частоту вращения, подачу и напор. Согласно уравнению (9-24), при заданных подаче Q и напоре Н более быстроходный насос будет иметь более высокую частоту вращения. Повышение частоты вращения ведет к снижению размеров и массы насоса и приводного двигателя. Уменьшение размеров и массы насоса и двигателя ведет, в свою очередь, к снижению габаритов здания НС зоподъемности кранового оборудования. Наблюдается тенденция к внедрению быстроходных насосов на более высокие напоры, Коэффициент быстроходности характеризует конструктивное исполнение рабочего колеса, в частности, соотношения их основных размеров, где D2 — выходной диаметр рабочего колеса и Do— входной диаметр. Лопастные насосы подразделяются на группы в соответствии со значением коэффициента быстроходности (табл. 9-1).
На рис. 9-15 даны эскизы рабочих колес насосов различной быстроходности. Следует заметить, что коэффициент быстроходности одинаков для колеса и насоса в случае только одноколесных насосов с односторонним входом жидкости на колесо.
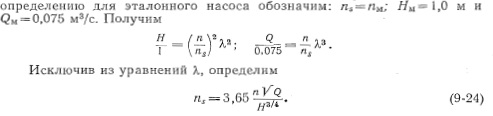
В многоступенчатых и многопоточных насосах коэффициент быстроходности можно определить как:
Для нормальной бескавитациоиной работы насоса необходимо, чтобы в пределах его проточного тракта давление было выше давления насыщенных паров перекачиваемой жидкости.
Иначе возникает кавитация, которая может привести к резкому падению КПД насоса, появлению шумов в проточном тракте и вибрации конструкций гидромашины и здания НС. При длительной работе насоса в условиях развитой кавитации возможны существенные разрушения элементов проточной части насоса. Наиболее подвержены кавитационному износу поверхности элементов, на которых возникает глубокий вакуум. Такими элементами в лопастных насосах являются прежде всего входные участки лопастей и камеры рабочего колеса. Так, например, проф. В. Я. Карелии приводит в 9-2 случай образования на поверхности камеры рабочего колеса крупного осевого насоса пояса кавитационного разрушения высотой до 110. мм и глубиной до 24 мм.
Определим условие возникновения кавитации на входе в насос. На рис. 9-16 показана схема насосной установки. Определим давление на входе в насос (сечение К — К), используя уравнение Бернулли и пренебрегая значением скоростного напора в сечении О—О.
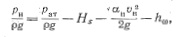
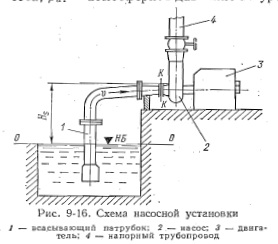
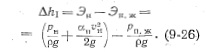

Избыток энергии Ahj называется кавитационным запасом или избыточным напором всасывания. Величина Ahi зависит от типа и конструкции насоса и изменяется при изменении режима его работы. Для обеспечения надежной бескавитационной эксплуатации насоса кавитационный запас увеличивают введением коэффициента (3, принимаемого для осевых насосов равным 1,15, а для центробежных—1,2—1,4.
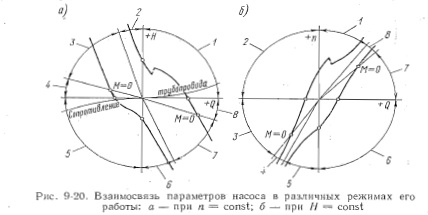
Все рассмотренные характеристики показывают взаимосвязи параметров насоса, работающего в нормальном насосном режиме. Они построены в одном квадранте и называются од но квадрант н ы м и. Однако насос может работать в широком диапазоне режимов, а при отключении двигателя от сети переходит в режим торможения, а затем в турбинный режим.
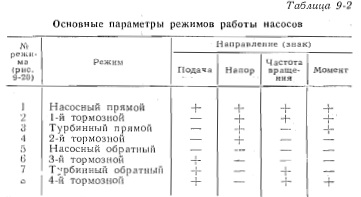
Взаимосвязь между основными параметрами во всех возможных режимах работы показывает круговая (полная) энергетическая характеристика насоса. Возможные режимы работы наcoca с указанием знаков их основных параметров даны в табл. 9-2 и на рис. 9-20, где 1—8 соответствует режиму по табл. 9-2. Направление параметров Н, Q, п, М в зоне нормального насосного режима примем за положительное. Все перечисленные в таблице режимы могут существовать лишь в установках, напор которых действует то с одной, то с другой стороны, например на ПЭС. Круговая характеристика строится в 4 квадрантах, поэтому ее называют четырех квадрантной. Обычно круговую характеристику представляют в безразмерном виде в координатах с нанесением линий приведенного момента
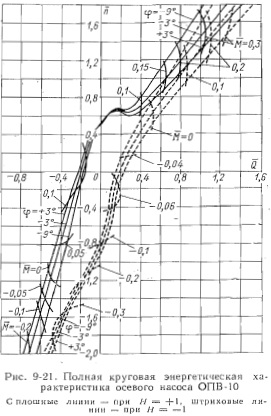
Для осевых поворотиолопастных вертикальных (ОПВ) насосов, серийно выпускаемых отечественной промышленностью, получены круговые характеристики 28-1, одна из которых представлена на рис. 9-21.
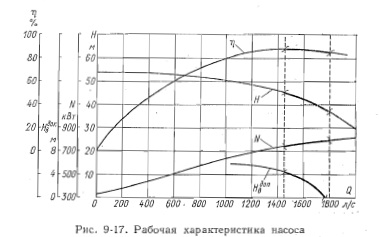
На действующих НС применяется эксплуатационная характеристика, на которой изолинии КПД насоса р и допустимых высот всасывания Hs даны в координатах напора и подачи при выбранных диаметре Dx и частоте вращения п. На характеристику наносится линия ограничения, которая при напорах ННР характеризует ограничение по мощности двигателя, а при низких напорах ограничение по водоподаче.
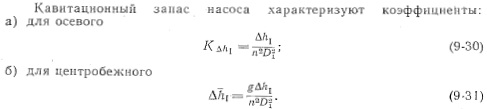
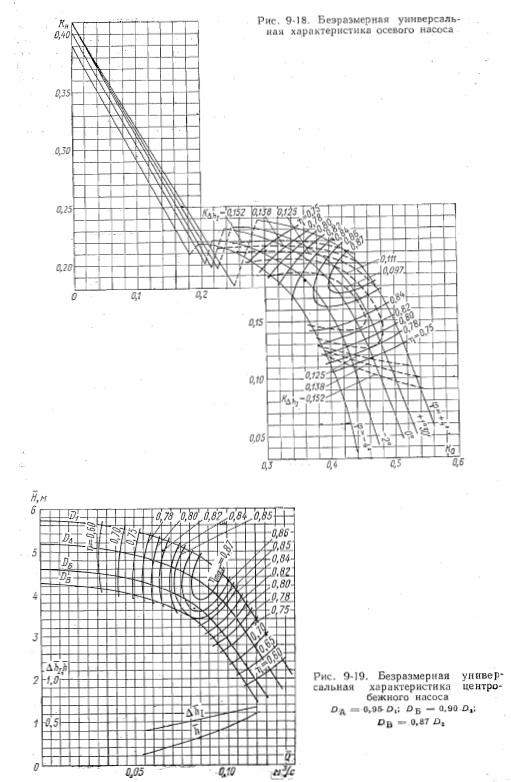
Эксплуатационная характеристика строится на основе универсальной характеристики.

При ее построении используются формулы подобия (9-16), (9-17) и (9-22).

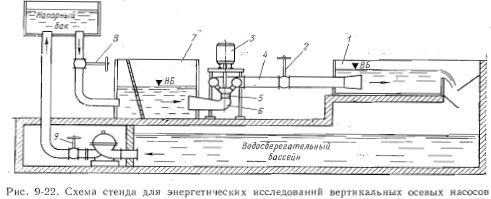
Характеристики насосов получают экспериментально на специальных стендах (более подробно — см. 9-7). В качестве примера приведем принципиальную схему стенда для энергетических исследований вертикальных осевых насосов в лаборатории гидроэнергетических установок ЛПИ
Подача насоса Q определяется с помощью индукционных, расходомеров, тарируемых объемным способом или по мерному водосливу. Развиваемый насосом напор определяется по показаниям манометров или пьезометров, снабженных стационарной шкалой. Режим работы насоса устанавливается с помощью регулировки реостата двигателя и задвижек 2,

В каждом исследуемом режиме работы насоса измеряются параметры Q, Н, Мк, ti а КПД вычисляется по формуле т = = 9,81 QH/N.
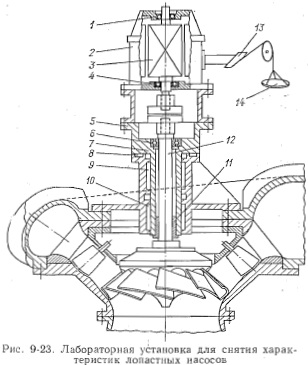
Как известно, при замере Мк, а следовательно, и rj наеоса значительную погрешность вносят силы трения подшипниковых опор балансирного подвеса статора электродвигателя. Этот недостаток устраняется в конструкции стенда для испытаний лопастных насосов рис. 9-23. Приводной электродвигатель 2 имеет ротор 3, установленный в подшипниках 1 и 4. Вал 12 испытуемого насоса вращается в подшипниках б и 11, расположенных в.балансирном подвесе 7, установленном на гидростатических опорах: 9 и 10 — радиальных и 8 — осевой. На фланце 5 осевой опоры установлен статор приводного электродвигателя. На статоре электродвигателя закреплен рычаг 13, связанный с ус-тройством 14 для измерения момента. При проведении испытаний обеспечивается возможность Рис. 9-23. Лабораторная установка для снятия харак- замера крутящего момента с теристик лопастных насосов точностью до потерь энергии на трение в гидростатических под-шипниках балансирного подвеса, которые ничтожно малы. При этом силы трения в подшипниках 1, 4, 6 и И являются внутренними силами системы и не влияют на точность измерения момента.
Целесообразно при исследованиях лопастных насосов применять подпружиненный направляющий аппарат 9-1, позволяющий ликвидировать люфт лопаток и повысить точ-ность испытаний,