
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПЕРЕХОДНЫХ ПРОЦЕССОВ В НС
Составим математическую модель переходных процессов в НС (рис. 20-3).
Электромагнитный переходный процесс в электрической машине опишем системой дифференциальных уравнений в форме, удобной для моделирования.


При изменении частоты вращения добавляется еще уравнение движения ротора, который состоит из вращающихся частей двигателя и насоса. Механический переходный процесс опишем уравнением движения ротора агрегата и, как предложено в [20-2], с учетом присоединенных масс жидкости в насосе
Гидравлический переходный процесс с учетом упругости воды и стенок напорных водоводов описывается уравнениями гидравлического удара (см. § 19-4). Однако, как показали исследования, выполненные в ЛГ1И [20-2], для НС с осевыми насосами и короткими волноводами, оборудованными сифонными водовыпусками, упругие свойства системы практически не влияют на характер переходных процессов.
В работах ряда исследователей указывается, что в ГЭУ при открытии и закрытии регулирующих органов за время упругость системы также практически не влияет на гидравлический удар: Поэтому условие «жесткого удара» (20-5) справедливо при решении ряда практических задач.
Уравнения (20-1), (20-2) и (20-5) являются моделью переходных процессов НС без учета упругих свойств системы.
Между электромагнитными, механическими и гидравлическими процессами существуют взаимосвязи. Однако они не всегда учитываются. Часто в практике используются упрощенные модели, позволяющие быстро решить задачу. Целесообразность упрощений всегда должна быть обоснована.
На рис. 20-4 показаны результаты расчета переходных процессов при отключении осевого насоса (Qp = 5M3/C) от сети. Не учет присоединенных масс (20-4) и инерционности жидкости (20-7) в данном случае приводит к завышению расчетной частоты вращения насоса в турбинном режиме на 28 %.
Решение уравнений, описывающих переходные процессы, производится, как правило, методом последовательных приближений. В этом случае уравнения представляются в форме конечных разностей. Расчет обычно выполняется с постоянным шагом At по времени, а в качестве неизвестной переменной принимается напор насоса. Начальным условием обычно считают установившийся режим работы агрегата.
Для моделирования переходных процессов в НС и ГАЭС используются ЭВМ. Составлены программы приближенного решения уравнений переходных процессов с теми или иными допущениями на цифровых ЭВМ различных поколений.
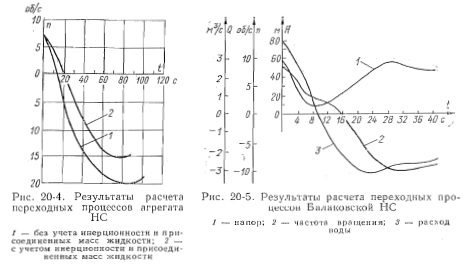
На рис. 20-5 представлены результаты расчета переходных процессов в Балаковской НС при аварийном отключении агрегата от электрической сети.
Переходные процессы возможно моделировать на аналоговых ЭВМ. При этом время проведения расчета резко сокращается до 6—10 с.
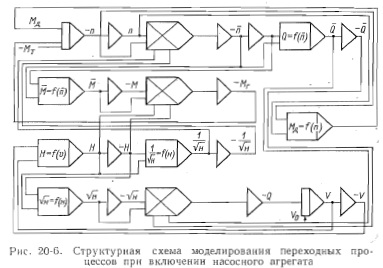
На рис. 20-6 дана структурная схема моделирования переходных процессов в НС при включении агрегата в сеть. При решении системы дифференциальных уравнений используется метод понижения порядка производной. Окончательная информация об исследуемом процессе выдается на двухкоординатные графопостроители и фиксируется в графической форме. За реализацией изучаемого процесса можно наблюдать визуально на экране индикатора и получать результаты в цифровой форме с помощью цифрового вольтметра и цифропечатающего устройства. Особенно целесообразно использовать аналоговые. ЭВМ для исследования особенностей протекания переходных процессов и влияния различных факторов на их характеристики.
